Prueba t de Student

DEFINICIÓN

Una variable con distribución t de Student se define como el cociente entre una variable normal estandarizada y la raíz cuadrada positiva de una variable 2 dividida por sus grados de libertad.Se aplica cuando la población estudiada sigue una distribución normal pero el tamaño muestral es demasiado pequeño como para que el estadístico en el que está basada la inferencia esté normalmente distribuido, utilizándose una estimación de la desviación tipica en lugar del valor real. Es utilizado en análisis discriminante.

Empleo de la prueba t de student

El test de locación de muestra única por el cual se comprueba si la media de una población distribuida normalmente tiene un valor especificado en una hipótesis nula.

El test de locación para dos muestras, por el cual se comprueba si las medias de dos poblaciones distribuidas en forma normal son iguales. Todos estos test son usualmente llamados test t de Student, a pesar de que estrictamente hablando, tal nombre sólo debería ser utilizado si las varianzas de las dos poblaciones estudiadas pueden ser asumidas como iguales; la forma de los ensayos que se utilizan cuando esta asunción se deja de lado suelen ser llamados a veces como prueba t de welch Estas pruebas suelen ser comúnmente nombradas como pruebas t desapareadas o de muestras independientes, debido a que tienen su aplicación mas típica cuando las unidades estadísticas que definen a ambas muestras que están siendo comparadas no se superponen.

El test de hipótesis nula por el cual se demuestra que la diferencia entre dos respuestas medidas en las mismas unidades estadísticas es cero. Por ejemplo, supóngase que se mide el tamaño del tumor de un paciente con cáncer. Si el tratamiento resulta efectivo, lo esperable seria que el tumor de muchos pacientes disminuyera de tamaño luego de seguir el tratamiento. Esto con frecuencia es referido como prueba t de mediciones apareadas o repetidas.

El test para comprobar si la pendiente de una regresión lineal difiere estadísticamente de cero.

Pruebas t para dos muestras apareadas y desapareadas

Las pruebas-t de dos muestras para probar la diferencia en las medias pueden ser desapareadas o en parejas. Las pruebas t pareadas son una forma de bloqueo estadístico, y poseen un mayor poder estadístico que las pruebas no apareadas cuando las unidades apareadas son similares con respecto a los "factores de ruido" que son independientes de la pertenencia a los dos grupos que se comparan. En un contexto diferente, las pruebas-t apareadas pueden utilizarse para reducir los efectos de los factores de confusión en un estudio observacional.

Desapareada

Las pruebas t desapareadas o de muestras independientes, se utilizan cuando se obtienen dos grupos de muestras aleatorias, independientes e idénticamente distribuidas a partir de las dos poblaciones a ser comparadas. Por ejemplo, supóngase que estamos evaluando el efecto de un tratamiento médico, y reclutamos a 100 sujetos para el estudio. Luego elegimos aleatoriamente 50 sujetos para el grupo en tratamiento y 50 sujetos para el grupo de control. En este caso, obtenemos dos muestras independientes y podríamos utilizar la forma desapareada de la prueba t. La elección aleatoria no es esencial en este caso, si contactamos a 100 personas por teléfono y obtenemos la edad y género de cada una, y luego se utiliza una prueba t bimuestral para ver en que forma la media de edades difiere por género, esto también sería una prueba t de muestras independientes, a pesar de que los datos son observacionales.

Apareada

Las pruebas t de muestras dependientes o apareadas, consisten típicamente en una muestra de pares de valores con similares unidades estadísticas, o un grupo de unidades que han sido evaluadas en dos ocasiones diferentes (una prueba t de mediciones repetitivas). Un ejemplo típico de prueba t para mediciones repetitivas sería por ejemplo que los sujetos sean evaluados antes y después de un tratamiento.

Una prueba 't basada en la coincidencia de pares muestrales se obtiene de una muestra desapareada que luego es utilizada para formar una muestra apareada, utilizando para ello variables adicionales que fueron medidas conjuntamente con la variable de interés.

La valoración de la coincidencia se lleva a cabo mediante la identificación de pares de valores que consisten en una observación de cada una de las dos muestras, donde las observaciones del par son similares en términos de otras variables medidas. Este enfoque se utiliza a menudo en los estudios observacionales para reducir o eliminar los efectos de los factores de confusión.

Cálculos

Las expresiones explícitas que pueden ser utilizadas para obtener varias pruebas t se dan a continuación. En cada caso, se muestra la fórmula para una prueba estadística que o bien siga exactamente o aproxime a una distribución t de Student bajo la hipótesis nula. Además, se dan los apropiados grados de libertad en cada caso. Cada una de estas estadísticas se pueden utilizar para llevar a cabo ya sea una prueba de una cola o prueba de dos colas.

Una vez que se ha determinado un valor t, es posible encontrar un valor o asociado utilizando para ello una tabla de valores de distribución t de Student. Si el valor p calulado es menor al límite elegido por significancia estadística (usualmente a niveles de significancia 0,10; 0,05 o 0,01), entonces la hipótesis nula se rechaza en favor de la hipótesis alternativa.

Prueba t para muestra única

En esta prueba se evalúa la hipótesis nula de que la media de la población estudiada es igual a un valor especificado μ₀, se hace uso del estadístico:

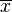t = \frac{\overline{x} - \mu_0}{s/\sqrt{n}},

donde

\overline{x}

es la media muestral, s es la desviación estándar muestral y n es el tamaño de la muestra. Los grados de libertad utilizados en esta prueba se corresponden al valor n − 1.

Pendiente de una regresión lineal

Supóngase que se está ajustando el modelo:

Y_i = \alpha + \beta x_i + \varepsilon_i,

donde x_i, i = 1, ..., n son conocidos, α y β son desconocidos, y ε_i es el error aleatorio en los residuales que se encuentra normalmente distribuido, con un valor esperado 0 y una varianza desconocida σ², e Y_i, i = 1, ..., n son las observaciones.
Se desea probar la hipótesis nula de que la pendiente β es igual a algún valor especificado β₀ (a menudo toma el valor 0, en cuyo caso la hipótesis es que x e y no están relacionados).
sea

\begin{align} \widehat\alpha, \widehat\beta & = \text{estimadores de cuadrados mínimos}, \\ SE_{\widehat\alpha}, SE_{\widehat\beta} & = \text{error estándar de los estimadores de cuadrados mínimos}. \end{align}

Luego

t_\text{valor} = \frac{\widehat\beta - \beta_0}{ SE_{\widehat\beta} }

tiene una distribución t con n − 2 grados de libertad si la hipótesis nula es verdadera. El error estándar de la pendiente:

SE_{\widehat\beta} = \frac{\sqrt{\frac{1}{n - 2}\sum_{i=1}^n (Y_i - \widehat y_i)^2}}{\sqrt{ \sum_{i=1}^n (x_i - \overline{x})^2 }}

puede ser reescrito en términos de los residuales:

\begin{align} \widehat\varepsilon_i & = Y_i - \widehat y_i = Y_i - (\widehat\alpha + \widehat\beta x_i) = \text{residuales} = \text{errores estimados}, \\ \text{SSE} & = \sum_{i=1}^n \widehat\varepsilon_i^{\;2} = \text{suma de los cuadrados de los residuales}. \end{align}

Luego

t_\text{valor}

se encuentra dado por: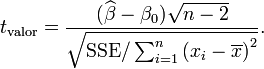

t_\text{valor} = \frac{(\widehat\beta - \beta_0)\sqrt{n-2}}{ \sqrt{\text{SSE}/\sum_{i=1}^n \left(x_i - \overline{x}\right)^2} }.

Prueba t dependiente para muestras apareadas

Esta prueba se utiliza cuando las muestras son dependientes; esto es, cuando se trata de una única muestra que ha sido evaluada dos veces (muestras repetidas) o cuando las dos muestras han sido emparejadas o apareadas. Este es un ejemplo de un test de diferencia apareada.

t = \frac{\overline{X}_D - \mu_0}{s_D/\sqrt{n}}.

Para esta ecuación, la diferencia entre todos los pares tiene que ser calculada. Los pares se han formado ya sea con resultados de una persona antes y después de la evaluación o entre pares de personas emparejadas en grupos de significancia (por ejemplo, tomados de la misma familia o grupo de edad: véase la tabla). La media (X_D) y la desviación estándar (s_D) de tales diferencias se han utilizado en la ecuación. La constante μ₀ es diferente de cero si se desea probar si la media de las diferencias es significativamente diferente de μ₀. Los grados de libertad utilizados son n − 1.

Par	Nombre	Edad	Test
Ejemplo de pares emparejados
1	Juan	35	250
1	Joana	36	340
2	Jaimito	22	460
2	Jesica	21	200

Número	Nombre	Test 1	Test 2
Ejemplo de muestras repetidas
1	Miguel	35%	67%
2	Melanie	50%	46%
3	Melisa	90%	86%
4	Michell	78%	91%

¿Cómo se deduce una distribución de “t”?

Extraigo K muestras de tamaño n < 30.
Calculo para cada muestra el valor de “t”.
Grafique la distribución para cada tamaño muestral

Distribución “t” para diferentes grados de libertad (n-1)

Condiciones:

· Se utiliza en muestras de 30 o menos elementos.

· La desviación estándar de la población no se conoce

Diferencias:

· La distribución t student es menor en la media y mas alta en los extremos que una distribución normal.

Tiene proporcionalmente mayor parte de su área en los extremos que la distribución normal.

Nivel de significación:

Grados de libertad:

· Existe una distribución t para cada tamaño de la muestra, por lo que “Existe una distribución para cada uno de los grados de libertad”.

· Los grados de libertad son el número de valores elegidos libremente.

· Dentro de una muestra para distribución t student los grados de libertad se calculan de la siguiente manera:

· GL=n – 1

EJEMPLO

Con un nivel de significancia de 5% se selecciona de manera aleatoria tres paquetes de croquetas (bultos) alimento para perros, de cada uno de los cinco pedidos. Al pesar los 15 paquetes se obtiene la media de = 49.4 y una desviación estándar de S²=1.2